A Netflix lançou no mês de março o seriado “O problema dos três corpos”. Nele, uma astrofísica chinesa consegue contacto com uma civilização alienígena que vive em um planeta iluminado por três sóis. Percorrendo uma trajetória caótica, o planeta ora é incinerado ora é congelado (Figura 1).

Figura 1 – Visão artística do sistema estelar triplo Gliese 667. Ele se encontra bem perto da Terra, a cerca de 22 anos-luz de distância, na direção da constelação de Escorpião. Hoje, no sistema Gliese 667, são conhecidos 6 exoplanetas, sendo que 3 deles se encontram em região habitável
O seriado se baseia na trilogia escrita pelo engenheiro chinês Liu Cixin. É uma ótima oportunidade para fazer contacto com a cultura chinesa e com o problema de três corpos, que há mais de 300 anos desperta o interesse e a imaginação de físicos e matemáticos.
O problema dos três corpos é um tema clássico e muito frequente na mecânica celeste. Considere um sistema em que 3 corpos se atraem mutuamente de acordo com a lei da gravitação de Newton. Dadas as posições e velocidades iniciais dos 3 corpos, será que é possível calcular, exata e analiticamente, esses valores num instante posterior qualquer? Salvo raras exceções, a resposta é não, pois o sistema é inerentemente caótico.

Figura 2 – Retrato de Isaac Newton em 1689, aos 46 anos. Ele formulou as 3 leis da mecânica e a teoria da gravitação universal em seu formidável livro “Philosophiae Naturalis Principia Mathematica”
Num sistema caótico, duas configurações iniciais mesmo que infinitesimalmente próximas, podem evoluir para configurações finais muito diferentes. Por exemplo, no problema dos 3 corpos, é possível que um deles seja expulso, ejetado, de maneira a afastar-se indefinidamente dos outros, reduzindo o sistema a um problema de 2 corpos (que tem solução analítica exata).
O estudo do problema dos 3 corpos trouxe resultados que são muito importantes. Entre eles, a utilização do efeito de estilingue gravitacional para as viagens espaciais, a determinação das trajetórias de asteróides e cometas que se aproximam da Terra e a utilização dos pontos de Lagrange para um posicionamento seguro dos nossos telescópios espaciais.
Considerações Iniciais
O sistema solar é estável? Era essa a pergunta que se fazia o matemático francês Henry Poincaré quando, no final do século 19, se inscreveu numa competição de mecânica celeste em comemoração ao sexagésimo aniversário do rei Oscar II da Suécia.
A questão proposta na competição dizia: “para um sistema com n partículas atraindo-se mutuamente segundo a lei da gravitação de Newton, supondo que duas dessas partículas nunca colidam, encontre uma expansão em série uniformemente convergente no tempo das coordenadas de cada partícula em termos de funções conhecidas”.
Poincaré enviou para a comissão julgadora um calhamaço de 300 páginas, ganhou a competição, mas não encontrou a solução. Entretanto, seu trabalho deu início a chamada teoria do caos.
A solução do problema de 3 corpos, como proposto na competição, foi obtida em 1912 pelo matemático finlandês Karl Sundman. A colisão de 2 corpos corresponde a presença de singularidades nas equações diferenciais. Sundman eliminou essas singularidades por um processo chamado de regularização. Ele apresentou sua solução na forma de uma série de Puiseux. A convergência é absurdamente lenta, precisando levar em conta 108.000.000de termos da série!
A aplicação da 2ª. lei de Newton ao problema dos 3 corpos resulta em um conjunto de 9 equações diferenciais de 2ª. ordem acopladas. Podemos integrar essas equações numericamente. Com os computadores modernos cada vez mais rápidos, podemos fazer previsões bem longínquas no tempo mesmo no caso das configurações caóticas.
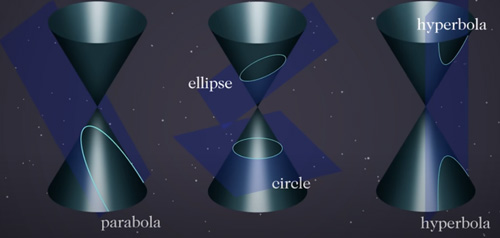
Figura 3 – As trajetórias permitidas no problema de 2 corpos são as chamadas curvas cônicas: círculo, elipse, parábola e hipérbole. Todas elas podem ser obtidas pela intersecção de um plano com um cone, daí seu nome. Qual dessas curvas os corpos vão percorrer depende da energia mecânica total inicial do sistema
Foi em 1687, no seu trabalho monumental: “Philosophiae Naturalis Principia Mathematica”, que Isaac Newton propôs a Teoria da Gravitação Universal e as suas três Leis de Movimento (Figura 2).
Na teoria da gravitação de Newton, duas partículas pontuais de massas m1 e m2 se atraem mutuamente com forças diretamente proporcionais ao produto dessas massas e inversamente proporcionais ao quadrado da distância entre elas. Essas forças têm a direção da reta que une as partículas e sentidos opostos.
Se os corpos não forem pontuais, mas sim, macroscópicos, deve-se utilizar cálculo integral e diferencial e levar em conta o caráter vetorial da força.
Na sua formulação original, a teoria pressupunha que a força gravitacional agia instantaneamente entre dois corpos, quaisquer que fossem as distâncias entre eles. Mas, como hoje sabemos que o campo gravitacional se propaga com a velocidade da luz, o cálculo da força gravitacional precisa levar em conta a distância entre os corpos e o correspondente atraso da informação.
A teoria da gravitação de Newton explicou, com total sucesso, as três leis empíricas obtidas pelo astrônomo Johannes Kepler ao investigar o sistema solar. Dessa forma, a teoria da gravitação de Newton ganhou o status de lei da gravitação de Newton. Entretanto, já no final do século XIX, a exatidão dessa teoria estava sendo questionada. Vejamos por quê.
Todos os planetas do sistema solar executam órbitas elípticas. O periélio é o ponto dessas órbitas em que o planeta está mais próximo do Sol. E o periélio de todos os planetas precessiona, isto é, gira com o passar do tempo. Por exemplo, o periélio da Terra ocorreu no dia 02 de janeiro de 2024 quando a direção Terra-Sol apontava para a constelação de Capricórnio. Daqui há 13 mil anos, ela terá girado 180 graus e apontará na direção da constelação de Câncer.
Levando-se em conta a perturbação gravitacional que os planetas exercem uns sobre os outros, as velocidades de precessão dos planetas puderam ser calculadas. Todas coincidiam, razoavelmente, com os resultados observacionais, exceto para o planeta Mercúrio. O valor calculado para Mercúrio era de 531 segundos de arco por século e o valor observado era de 574 segundos de arco por século (ou 1 grau a cada 627 anos). A diferença só foi explicada com a Teoria da Relatividade Geral proposta por Albert Einstein em 1915.
Podemos afirmar que a teoria da gravitação de Newton é boa, mas, falha na presença de campos gravitacionais muito intensos como aqueles criados nas proximidades de estrelas ou buracos negros. A teoria não prevê a existência dos buracos negros, a curvatura da luz ao passar por corpos celestes muito massivos e nem a dilatação temporal (o tempo passa mais devagar em regiões com campos gravitacionais mais intensos).
O problema dos 2 corpos
Suponha duas partículas de massas m1 e m2 se atraindo mutuamente segundo a lei da gravitação de Newton. As forças gravitacionais entre elas têm mesmo módulo, direção e sentidos opostos. Na ausência de forças externas, a força resultante é nula, o que implica que o centro de massa tem aceleração zero, ou seja, ele se move com velocidade constante.
Como a força gravitacional tem a direção da reta que une as duas partículas ela é uma força central. Forças centrais não produzem torque e, portanto, conservam o vetor momento angular total do sistema. Consequentemente, os dois corpos podem apenas se movimentar no plano que é perpendicular ao vetor momento angular total do sistema.
O problema de 2 corpos tem solução analítica exata. Escolhendo o centro de massa como a origem do sistema de coordenadas e utilizando coordenadas relativas ao centro de massa, o problema de 2 corpos se reduz ao problema de 1 corpo só com a chamada massa reduzida m1m2/(m1+m2).
As trajetórias permitidas podem ser circulares, elípticas, parabólicas ou hiperbólicas. São as chamadas curvas cônicas (Figura 3). Como as forças gravitacionais são conservativas, a energia mecânica total do sistema E (que é a soma da energia cinética com energia potencial gravitacional) é constante no tempo. Se E < 0, teremos trajetórias elípticas (ou circular, se a excentricidade da elipse for zero); se E = 0, ela será parabólica e se E > 0, ela será hiperbólica.
O problema dos 3 corpos
Tão logo o problema de 2 corpos foi resolvido, as atenções se voltaram para próxima etapa: o problema dos 3 corpos.
Quando passamos para um sistema com 3 corpos interagindo gravitacionalmente, quais os resultados de 2 corpos que continuam valendo? A resposta é simples: as constantes de movimento. Explicitamente: o vetor velocidade do centro de massa, o vetor momento angular total do sistema e a energia mecânica total.
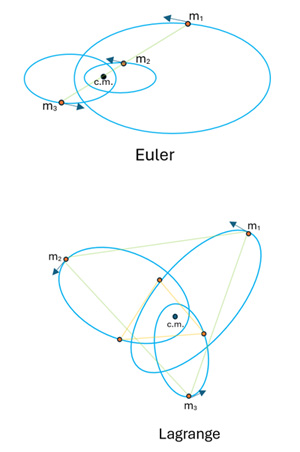
Figura 4 – Soluções periódicas de configurações centrais. As massas m1, m2 e m3 são arbitrárias. Euler: as massas executam órbitas elípticas em torno do centro de massa (c.m.) sempre mantendo o alinhamento (linha verde) dos 3 corpos. Lagrange: as massas executam órbitas elípticas em torno do centro de massa e estão dispostas formando um triângulo equilátero (linha verde). Com o tempo, os lados do triângulo equilátero se modificam dinamicamente (linha laranja)
A trajetória de cada um dos 3 corpos dependerá, de maneira crucial, da inicialização do sistema, ou seja, das posições e das velocidades atribuídas inicialmente a cada um dos corpos. Teremos soluções periódicas e também soluções caóticas. Lembrando que, no problema de 2 corpos, não existem soluções caóticas, somente soluções periódicas (elípticas) e não-periódicas (parabólicas ou hiperbólicas).
*As soluções periódicas de Euler e Lagrange
Euler, em 1767, e Lagrange, em 1772, encontraram soluções periódicas
para o problema de 3 corpos que são do tipo configurações centrais. Nessas configurações centrais, as acelerações dos 3 corpos apontam sempre para o mesmo ponto – o centro de massa do sistema.
Na solução de Euler, os 3 corpos permanecem sempre ao longo de uma mesma linha reta e percorrem elipses diferentes, mas, confocais (Figura 4). As elipses têm mesma excentricidade e o foco comum delas está localizado no centro de massa. A solução de Euler é instável e se desfaz com qualquer pequena perturbação.
Na solução de Lagrange, os 3 corpos estão sempre formando um triângulo equilátero. Aqui também, os corpos evoluem ao longo de elipses diferentes, mas, com a mesma excentricidade e mesmo foco (localizado no centro de massa). Há tanto regiões de estabilidade quanto de instabilidade.
Para um encaminhamento bem bacana dessas soluções (hoje históricas) veja aqui.
*O problema restrito dos 3 corpos
O problema restrito dos 3 corpos é um caso especial do problema geral quando um deles tem massa muito menor do que a dos outros dois. Como a aceleração gravitacional provocada pelo corpo pequeno sobre os outros é desprezível, os dois corpos massivos se movimentam sentindo apenas a presença um do outro. Dessa forma, os corpos massivos percorrerão círculos ou elipses em torno do centro de massa mútuo (que é, basicamente, o centro de massa dos 3 corpos). Eles correspondem ao problema circular restrito e ao problema elíptico restrito, respectivamente. Focaremos o caso circular por ele ser mais simples e muito mais estudado. O caso elíptico você encontra aqui.
No problema circular restrito de 3 corpos escolhe-se um sistema de coordenadas sinódico, com origem no centro de massa e que rotaciona com velocidade angular uniforme no plano de órbita e junto com os 2 corpos massivos. Neste sistema de coordenadas, os 2 corpos massivos estão parados (coisa que não acontece no caso elíptico). Trata-se, portanto, de um referencial não inercial, e nele aparecerão forças centrífugas e forças de Coriolis. Além disso, nesse referencial, há também uma lei de conservação – a constante de Jacobi.
Neste sistema existem pontos em que as forças gravitacionais e centrífugas se anulam. São 5 pontos de equilíbrio conhecidos como pontos de Lagrange.
Cada par de corpos celestes massivos têm o seu próprio (e diferentes) conjunto de pontos de Lagrange: Terra-Sol (veja Figura 5), Terra-Lua, Saturno-Sol, Saturno-Titã etc.
Um aspecto muito importante dos pontos de Lagrange trata da estabilidade desses pontos. Se o corpo pequeno for ligeiramente afastado dos pontos de equilíbrio de Lagrange, ele retornará ou se afastará?
Os pontos L1, L2 e L3 são pontos instáveis, mais especificamente, eles são pontos de cela pois têm máximo em uma direção e mínimo em outra. Naves ou satélites localizados nesses pontos precisarão fazer manobras para permanecerem na posição.
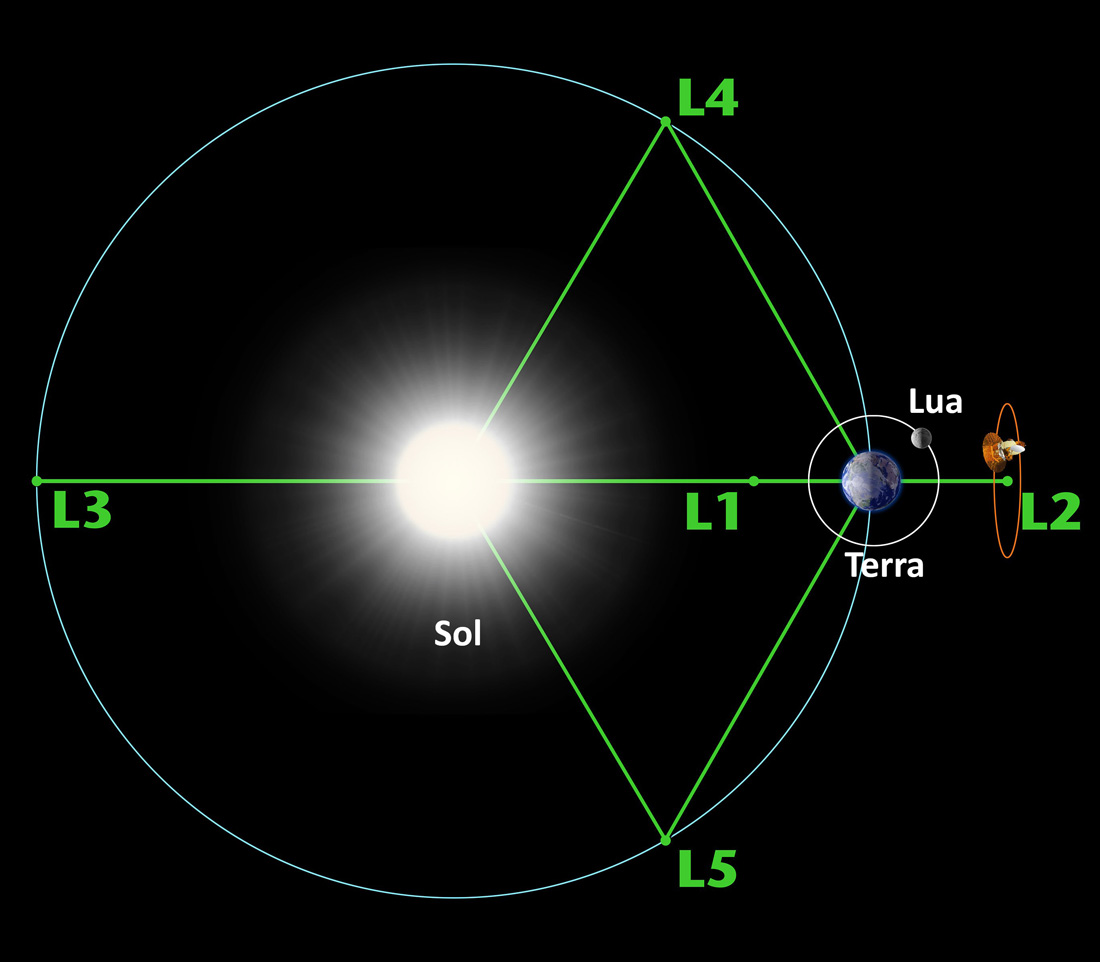
Figura 5 – Sistema Terra-Sol. Os pontos de Lagrange L1, L2 e L3 estão ao longo da linha Terra-Sol. Suas distâncias aproximadas, a partir do centro da Terra: L3 trezentos milhões de quilômetros; L1 e L2 um milhão e 500 mil quilômetros. Entre o Sol e a Terra, no ponto L1 , está o satélite Deep Space Climate Observatory (https://en.wikipedia.org/wiki/Deep_Space_Climate_Observatory) que estuda os ventos solares. Depois da órbita da Lua, no ponto L2, estão os telescópios James Webb (https://en.wikipedia.org/wiki/James_Webb_Space_Telescope) e Euclid (https://en.wikipedia.org/wiki/Euclid_(spacecraft)). Os pontos L4 e L5 formam com o Sol e a Terra um triângulo equilátero e, portanto, estão a 150 milhões de quilômetros do centro da Terra. O ponto L3 está tão longe que qualquer corpo lá localizado sofreria muito mais influência de Vênus do que da própria Terra
Os pontos L4 e L5 são estáveis desde que a razão entre as massas dos dois corpos massivos seja maior do que 24,96 (que é o caso do sistema Terra-Sol).
Devido a essa estabilidade, são nos pontos L4 e L5 que encontramos os asteróides troianos. Eles acompanham um planeta (qualquer planeta), percorrendo a mesma órbita deste. Alguns vão à frente, outros seguem atrás do planeta. Quase todos os planetas do sistema solar têm seus asteróides troianos. A Terra tem 2 asteróides troianos conhecidos: o 2010TK7, que tem diâmetro de 300 metros e o 2020XL5, cujo diâmetro é de 1,2 km. Ambos seguem à frente da Terra próximos do ponto L4.
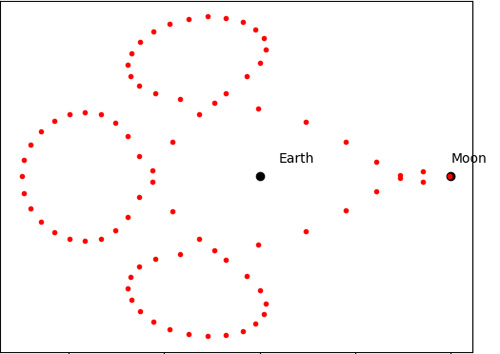
Figura 6 – A órbita de Arenstorf (https://pymgrit.github.io/pymgrit/applications/arenstorf_orbit.html) com a Terra no centro e a Lua à sua direita. Ela é uma órbita periódica e fica no plano de rotação do sistema Terra-Lua
O problema circular restrito dos 3 corpos tem infinitas soluções periódicas e infinitas soluções caóticas. A NASA, através do Jet Propulsion Laboratory, disponibiliza centenas de milhares de órbitas periódicas conhecidas para vários sistemas: Terra-Sol, Terra-Lua, Sol-Marte etc.
Na Figura 6 mostramos a órbita de Arenstorf. Ela foi utilizada pela NASA para salvar a tripulação da Apolo 13. Essa órbita permitiu à espaçonave permanecer próxima do ponto de Lagrange L1 (do sistema Terra-Lua), consumindo um mínimo de combustível.
A técnica da gravidade assistida é outro resultado importante do problema circular restrito dos 3 corpos. Utilizando a gravidade dos planetas, essa técnica permite manobrar espaçonaves tanto para aumentar quanto para diminuir a sua velocidade, poupando, em ambos os casos, combustível.
Essa técnica foi utilizada pela primeira vez em 1959 quando a sonda soviética Luna 3 alcançou o lado oculto da Lua.
Vou tentar explicar a gravidade assistida de maneira não quantitativa utilizando apenas análise vetorial e mudança de referencial, seguindo este texto da NASA.
Considere uma espaçonave se aproximando do planeta Júpiter.
Na Figura 7 (a), a espaçonave se aproxima do planeta por trás, no mesmo sentido da órbita de Júpiter em torno do Sol. No referencial de Júpiter, a velocidade da nave muda apenas de direção, mas, não de módulo (vetor azul v). No referencial do Sol, Júpiter tem velocidade v´ (verde) e a velocidade da nave será a soma vetorial v + v´ (pela regra do paralelogramo). Vemos que a velocidade final da nave Vf é maior do que a sua velocidade inicial Vi. A nave aumentou a velocidade, é o efeito estilingue gravitacional.
Na Figura 7 (b), a espaçonave se aproxima do planeta pela frente, no sentido oposto ao da órbita de Júpiter em torno do Sol. Vemos que a velocidade final da nave Vf é menor do que a sua velocidade inicial Vi. A nave diminuiu a velocidade, é um freio gravitacional.
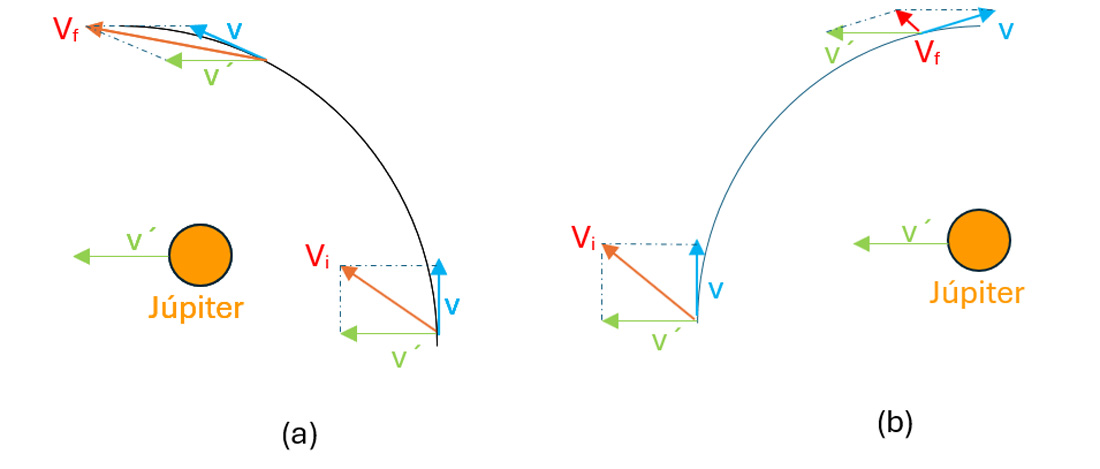
Figura 7 – (a) Efeito estilingue gravitacional; (b) Efeito freio gravitacional
Para ilustrar esse efeito de maneira realística e quantitativa, apresentamos, na Figura 8, o aumento de velocidade da nave Voyager 2 quando ela se aproximou dos planetas Júpiter, Saturno, Urano e Netuno. Sem o estilingue gravitacional ela só chegaria até Júpiter e não conseguiria sair do sistema solar.
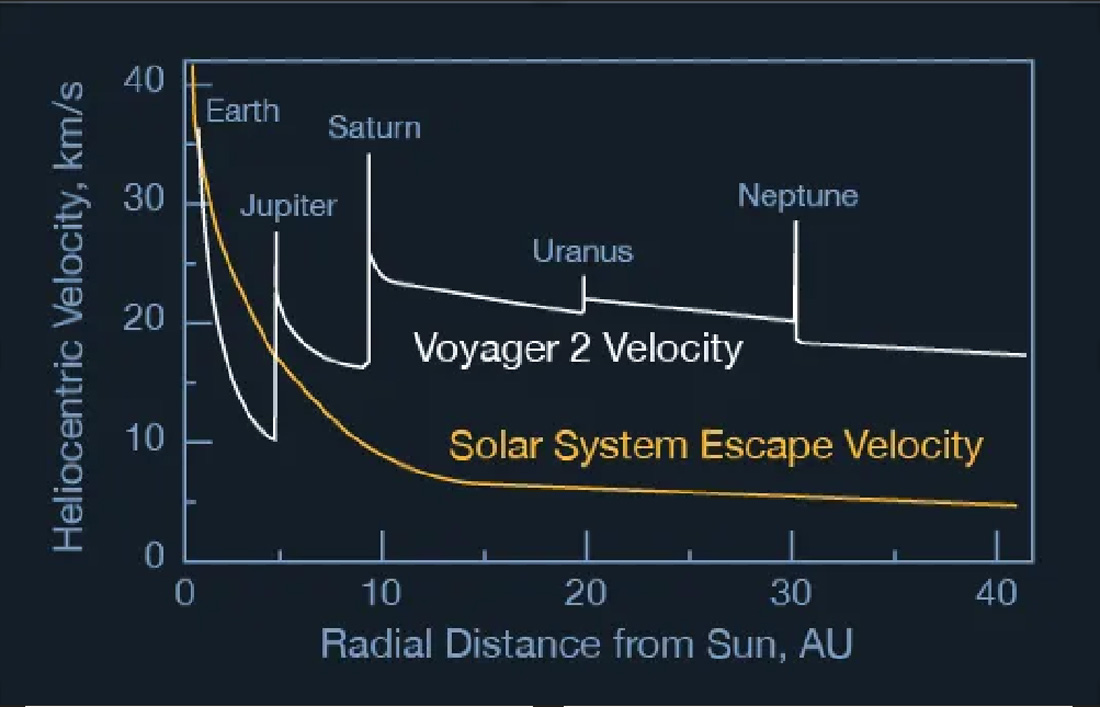
Figura 8 – Gráfico da velocidade em relação ao Sol (em km/s) versus distância ao Sol (em unidade astronômica ~ 150 milhões de km) da nave Voyager 2. Em amarelo, a velocidade de escape para a Voyager 2 conseguir sair do sistema solar. Fonte: Steve Matousek, JPL
(Continua na parte 2 – em breve)
Para acessar todo o conteúdo do site “Notícias de Ciência e Tecnologia”, clique AQUI.
Para acessar todo o conteúdo do site “Newsletter – Ciência em Panorama” clique AQUI.
*Físico, Professor Sênior do IFSC – USP / e-mail: onody@ifsc.usp.br
(Agradecimento: ao Sr. Rui Sintra da Assessoria de Comunicação)
Assessoria de Comunicação – IFSC/USP



