
Figura 1 – O matemático alemão Lothar Collatz (1910 – 1990), autor da conjectura (Crédito: MFO e Konrad Jacobs)
Por: Prof. Roberto N. Onody *
Em 1937, dois anos depois de defender seu doutorado, o alemão Lothar Collatz (Figura 1), formulou uma hipótese matemática que segue, até hoje, não demonstrada. Pela sua simplicidade, a conjectura tem atraído matemáticos profissionais e amadores, que tentam provar a sua veracidade. Todos consideram o problema “perigoso”. Perigoso porque é apaixonante e envolvente. Muitos cientistas passaram anos, décadas, tentando resolvê-lo, inutilmente. Durante a guerra a fria, se dizia que o problema foi inventado pelos soviéticos para atrasar a ciência nos EUA.
A dinâmica de Collatz é muito simples, são apenas 2 regras. Escolha um número natural qualquer N (1, 2, 3, …)
-Se N for par, divida por 2 —> N/2
-Se N for ímpar, multiplique por 3 e adicione 1 —> 3N + 1
Se aplicarmos essas regras, por exemplo, para o número N = 17, ele evoluirá da seguinte maneira:
17 à 52 à 26 à 13 à 40 à 20 à 10 à 5 à 16 à 8 à 4 à 2 à 1
Ao chegar ao número 1, a dinâmica entra num ciclo 3 (1, 4, 2, para sempre)
A Conjectura de Collatz afirma que: “Todo e qualquer número natural, terminará sua dinâmica no ciclo 3”.
Portanto, provar a Conjectura de Collatz significa demonstrar que, iniciando o processo com qualquer número natural, não importando o  seu tamanho, ele acabará no ciclo 3.
seu tamanho, ele acabará no ciclo 3.
Claro, a primeira coisa que se pensa é em usar a força bruta computacional. Em 2020, a conjectura foi testada para todos os números naturais de 1 até 268 ~ 3 1020. Todos convergiram para o ciclo 3 1.
Obviamente, nenhum matemático aceita esse resultado numérico como prova da conjectura. Ele só prova que, até esse número, ela está correta. Porém, podem existir números muito maiores, que levem a dinâmica ao infinito. Ou ainda, que conduza a um conjunto de números gigantescos que formem um outro e novo ciclo. Com o número 268 nas mãos, matemáticos provaram que, se existir um ciclo acima dele, este ciclo tem que ser gigantesco e composto por, pelo menos, 186 bilhões de números!
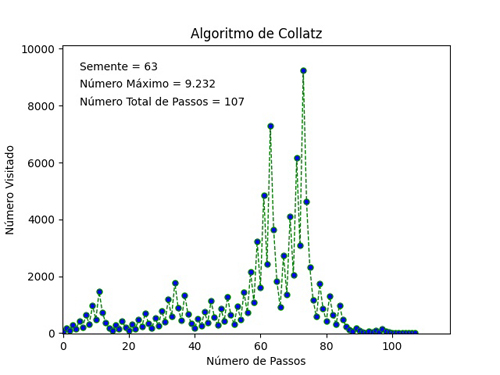
Figura 2 – Evolução da dinâmica de Collatz para N = 63 (Crédito: R. N. Onody)
Muito embora, os matemáticos saibam ser possível apresentar provas computacionais e numéricas na solução de algumas conjecturas matemáticas (veja ref.2 ), esse não parece ser o caso aqui. Contra a força bruta, eles têm o episódio da Conjectura de Pólya. Todo número natural maior do que 1, pode ser decomposto em um número par ou ímpar de produto de números primos. Dessa forma, 16 é par (4, 16 = 2.2.2.2), 8 é ímpar (3, 8 = 2.2.2), 17 é ímpar (1) e assim por diante. Podemos então, contar até um certo número natural N, quantos se decompõem em números pares e ímpares. Por exemplo, até N = 20, 12 são ímpares e 7 são pares. Em 1919, o matemático húngaro George Pólya, propôs a conjectura de que o conjunto de números naturais com decomposição par é sempre maior ou igual ao dos ímpares. Foi somente em 1958, que C. B. Haselgrove provou a existência de um contraexemplo para N = 1,845 10361 ! 3
Claro, bastaria um contraexemplo para quebrar a Conjectura de Collatz pois, a sua dinâmica é muito sensível à semente (inicialização). Por exemplo, para N = 63, a dinâmica chega até o número 9.232 e leva 107 passos até o ciclo (Figura 2); já para a semente N = 64, este é também o valor máximo, chegando ao ciclo em 6 passos (Figura 3) 4. Há explosões na dinâmica de Collatz, que nos fazem acreditar ser possível encontrar um contraexemplo. A Semente 9.663 atinge o máximo de 27.114.424 antes de recuar para o ciclo.
Se considerarmos a dinâmica de Collatz para os números inteiros negativos, obteremos pelo menos 3 ciclos: (-1, -2); (-5, -14, -7, -20, -10); e (-17, -50, -25, -74, -37, -110, -55, -164, -82, -41, -122, -61, -182, -91, -272, -136, -68, -34), com número de elementos 2, 5 e 18, respectivamente. Curiosamente, esses mesmos ciclos (com sinais positivos) aparecem se alterarmos a regra 3N + 1 para 3N – 1, mas ainda permanecendo no âmbito dos números naturais positivos.
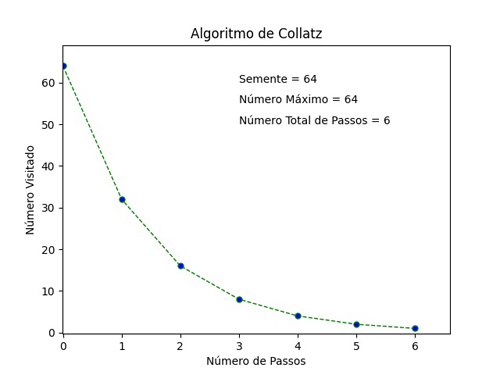
Figura 3 – Evolução da dinâmica de Collatz para N = 64 (Crédito: R. N. Onody)
Muito embora não exista hoje uma prova da conjectura de Collatz, há resultados parciais bem interessantes. Um dos mais brilhantes matemáticos da atualidade, Terence Tao 5, demonstrou, em 2019, o seguinte teorema: “Quase todos os valores iniciais N (sementes), quando iterados pela dinâmica de Collatz, têm valor menor do que f(N), para qualquer função f(N) que vá a infinito quando N tende a infinito, não importando quão lentamente f(N) cresce ”. Por qualquer função de crescimento lento, você pode pensar coisas como log(log(log(log(N)))). Para os matemáticos, quase todos significa 99,99… % (adicione quantos noves quiser). Muito convincente, é uma quase prova, mas não é uma prova.
Sobre a conjectura de Collatz, o matemático húngaro Paul Erdös declarou em 1983: “A matemática ainda não está madura para resolver esse problema”.
*Físico, Professor Sênior do IFSC – USP
(Agradecimento: ao Sr. Rui Sintra da Assessoria de Comunicação)
Referências:
1 Collatz conjecture – Wikipedia
2 A Solução da Conjectura de Keller – verdadeira, ou falsa? – Portal IFSC (usp.br)
3 Porém, com o advento dos computadores, M. Tanaka encontrou (em 1980) o menor número que viola a Conjectura de Pólya, N = 906.150.257
4 Caso tenha interesse, escrevi a Conjectura de Collatz em Python e também uma versão executável para Windows (sem vírus ). Você pode solicitar por e-mail.
5 The Notorious Collatz conjecture (wordpress.com)
Rui Sintra – Assessoria de Comunicação – IFSC/USP



