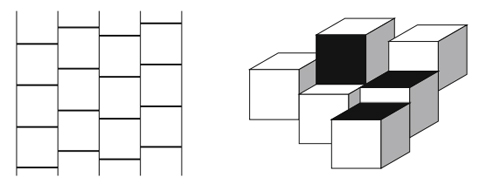
Figura 1 – À esquerda: espaço 2-dimensional, ao ser coberto por quadrados, sempre haverá arestas (face 1-dimensional) de dois quadrados diferentes, representadas por linhas mais grossas na figura, totalmente coincidentes. À direita: espaço 3-dimensional, ao ser coberto por cubos, sempre haverá quadrados (face 2-dimensional) de dois cubos diferentes, representados pela cor preta na figura, totalmente coincidentes – Crédito: J.Brakensiek et al 1
Por: Roberto N. Onody*
Um cubo A (também chamado, às vezes, de hipercubo) em n dimensões tem todas as arestas iguais a b e volume bn. Suas faces têm dimensão (n-1). Supondo que esses cubos A são maciços (isto é, que eles não possam se interpenetrar), dizemos que cobrimos um espaço de dimensão n com esses cubos A, se e somente se, todos os pontos desse espaço estão no interior de algum cubo ou nas suas faces de contacto (veja figura 1). Não poderá haver lacunas no espaço.
Um cubo, centrado na origem do sistema de coordenadas, tem todos os seus pontos representados por uma n-upla (x1 ,x2 ,…,xn) de números reais tais que xi está no intervalo fechado [-b/2,b/2], i = 1,…n . O número de faces de dimensão n-1 é 2n e o número de vértices é 2n. Para cobrir o espaço n-dimensional, colocamos (justapomos) um número infinito de cubos idênticos, mas com centros diferentes, que poderão ser transladados, nas faces de contacto, em qualquer uma das n direções e nos dois sentidos.
Em 1930, H. O. Keller propôs sua conjectura: “Num espaço n-dimensional, a justaposição de cubos para cobrir todo o espaço, sempre existirá um par de cubos que compartilharão uma face completa (inteira) de dimensão (n-1)”.
Em 1940, O. Perron provou que a conjectura de Keller é verdadeira para n menor ou igual a 6. Em 2002, J. Mackey provou que a conjectura é falsa para n maior ou igual a 8. E para n = 7 ?. A resolução, para essa dimensão, veio somente agora em 2020 1.
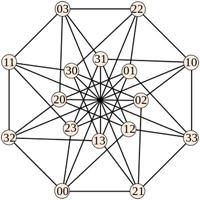
Figura 2 – O grafo de Keller – Crédito: Wikipédia
Em 1990, Corrádi e Szabó demonstraram que para verificar a conjectura de Keller era necessário e suficiente estudar os grafos de Keller 2.
Seja n a dimensão do espaço que queremos cobrir. Definimos um conjunto {a1,a2 ,…, an} onde as variáveis ai podem assumir qualquer um dos 2s valores inteiros {0,1,2,…,2s-1}. Obviamente, este conjunto conterá (2s)n vértices. Para formar um grafo de Keller, precisamos definir quando dois vértices são adjacentes, isto é, quando eles estão ligados por uma aresta. Dois vértices são adjacentes, se e somente se, eles diferem exatamente de s em pelo menos uma das coordenadas e são diferentes em pelo menos duas coordenadas. Por exemplo, considerando o grafo de Keller G3,2 , os vértices (0 1 2), (0 3 1), (2 3 0) estão todos ligados entre si , enquanto que os vértices (0 1 2),(0 3 2), (0 2 3) não têm nenhuma ligação entre si. Veja a figura 2 para um grafo de Keller com todas as suas ligações 3.
Um clique de um grafo com um número de vértices igual a V, é um subconjunto com número de vértices V’, V ‘ menor ou igual a V, de tal forma que todos os vértices de V ‘ que compõe o clique estejam ligados entre si.
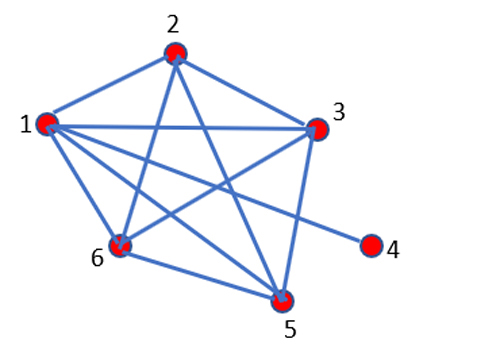
Na figura 3, V = 6, há cliques com tamanho 3 [(123), (136), (356), …], tamanho 4 [(1236), (1256), (2356), …] e um único clique de tamanho 5 (12356) que é, portanto, o clique máximo.
Já na figura 2, que é o grafo de Keller G2,2, só existem cliques de tamanho 2 (V = 16, V ‘= 2). O clique máximo é, portanto, igual a 2. Na verdade, o clique máximo é igual a 2 para todos os valores de s dos grafos G2,s , s = 1,2,…
Corrádi e Szabó provaram, em 1990, que a conjectura de Keller é falsa se e somente se o clique máximo de Gn,s tiver o tamanho 2n.
No caso n = 7, Kisielewicz demonstrou que a conjectura de Keller é verdadeira se e somente se não existir, no grafo G7,3 , clique com tamanho 27. E é nesse ponto que entra o trabalho de Brakensiek et al 1. recém publicado. Usando de força bruta computacional eles demonstraram que não existe nenhum clique com tamanho 27 na dimensão n = 7.
Em resumo, a conjectura de Keller é verdadeira para n menor ou igual a 7 e é falsa para n maior ou igual a 8.
Referências:
1 Brakensiek J., Heule M., Mackey J., Narváez D. (2020) The Resolution of Keller’s Conjecture. In: Peltier N., Sofronie-Stokkermans V. (eds) Automated Reasoning. IJCAR 2020. Lecture Notes in Computer Science, vol 12166. Springer, Cham.
https://doi.org/10.1007/978-3-030-51074-9_4
2 https://phys.org/news/2020-10-scientists-year-old-geometry-problem.html
3 https://en.wikipedia.org/wiki/Keller%27s_conjecture
*Físico, Professor Sênior do IFSC – USP
(Agradecimento: Sr. Rui Sintra da Assessoria de Comunicação)
Assessoria de Comunicação – IFSC/USP
