
Sobre damas, xadrez e computadores (Crédito: Domínio Público)
Por: Prof. Roberto N. Onody *
No xadrez, a dama é a peça que tem maior mobilidade e alcance. Ela pode se movimentar pelas linhas, colunas e diagonais do tabuleiro.
Em 1848, o enxadrista Max Bezzel [1], especializado em montar e analisar finais de jogos de xadrez (por exemplo, xeque-mate em 2 lances) propôs o seguinte problema: num tabuleiro de xadrez vazio, de quantas maneiras diferentes se pode dispor 8 damas de modo que nenhuma delas esteja sendo atacada?
O problema foi resolvido, por análise combinatória, dois anos depois por Franz Nauck. Existem 92 configurações que solucionam o problema. Na Figura 1, apresentamos uma dessas configurações. Sem dúvida, esse problema das 8 damas é perfeitamente talhado para programas computacionais. Veja a solução em linguagem Python [2].
Quando aprendi os rudimentos do jogo de xadrez (ok, foi há muito tempo, na década de 60) os grandes enxadristas para mim eram Alexander Alekhine e Jose Raul Capablanca. Segundo o site chess.com [3], eles estão classificados em 10o e 4o lugar, respetivamente. Em primeiro lugar está o russo Garry Kasparov, seguido do norueguês Magnus Carlsen, atual campeão mundial (título conquistado no ano passado, pela 5a vez). O primeiro campeão mundial de xadrez foi o tcheco Wilhelm Steinitz em 1886.
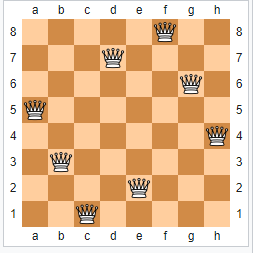
Figura 1 – Uma solução particular do problema das 8-damas. Com rotação de 90o e reflexões horizontal e vertical, mais 3 soluções podem ser geradas (Crédito: Wikipedia)
Naturalmente, a lista dos melhores enxadristas apresentadas no site chess.com [3] se baseia, vamos dizer assim, no gosto pessoal dos seus membros ativos. A Federação Internacional de Xadrez, FIDE (Fédération Internationale des Échecs) [4] que tem sede na Suíça, é quem coordena os principais torneios internacionais. Nesses torneios, os jogadores recebem uma pontuação (que depende da sua classificação no torneio). Para ser um Mestre Internacional, o enxadrista precisa acumular 2.400 pontos e 2.500 para se tornar Grande Mestre. Esses títulos, atribuídos ao enxadrista, valem por toda a sua vida, mesmo que sua pontuação acumulada diminua com o tempo.
Hoje, há mais de mil Grandes Mestres vivos no mundo, sendo 14 deles brasileiros. O mais jovem Grande Mestre (até agora) é o norte-americano Abhimanyu Mishra , com 12 anos e 4 meses (obteve o título em junho/2021). O atual campeão brasileiro é Luís Paulo Supe e a campeã brasileira é Júlia Alboredo (ambos conquistaram seus títulos no campeonato brasileiro de 2021, em 2020 não houve campeonato devido à pandemia).
Um critério menos subjetivo para classificar os enxadristas, seria através do pico (máximo) de sua pontuação ao longo de toda a sua carreira. Neste caso, o primeiro lugar caberia a Carlsen (até aqui, 2.889 pontos) e o segundo lugar a Kasparov (2.856 pontos, ele se aposentou em 2005).
E há sempre novos e ótimos enxadristas surgindo. No dia 22/02/2022, Carlsen perdeu o torneio de Airthings Masters para o indiano Rameshbabu Praggnanandhaa, um talento precoce de apenas 16 anos. Ele é o mais jovem enxadrista a derrotar Carlsen.
Entre as mulheres, a primeira enxadrista no ranking da FIDE é a chinesa Yifan Hou, com 2.658 pontos (em fevereiro/2022).
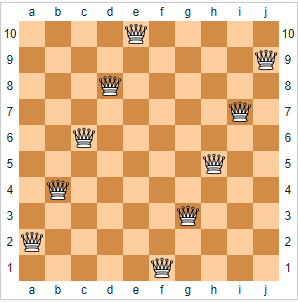
Figura 2 – Uma solução tipo degrau de escada do problema das 10-damas (Crédito: Wikipedia)
A FIDE se tornou a primeira federação internacional esportiva a lançar seu próprio NFT (Non-Fungible Tokens). Um token não fungível utiliza a tecnologia blockchain e é negociado em criptomoedas. Ao contrário de uma determinada criptomoeda (como bitcoins, ethereuns…), que são todas iguais entre si e têm o mesmo valor (como as notas de 100 reais, por exemplo), um NFT é exclusivo e único. É muito comum em games, onde um jogador compra um NFT para ter personagens ou avatares exclusivos e únicos no mundo todo. A FIDE já disponibilizou a compra de NFTs para os melhores momentos do Campeonato Mundial de Xadrez, realizado em Dubai em 2021.
Na minha opinião, o xadrez conheceu o seu auge na década de 1970, durante a guerra fria, no embate entre o norte-americano Bobby Fisher e a poderosa escola de xadrez da Rússia.
Depois disso, o xadrez manteve ainda uma certa popularidade, graças ao início do confronto homem x computador. A primeira vez que um programa de xadrez participou de um torneio foi em 1967. O algoritmo era o Mac-Hack VI (escrito por Richard Greenblat, analisava 10 posições por segundo) e bateu um enxadrista de ranking 1510. O programa Deep-Thought foi o primeiro a vencer um Grande Mestre (o enxadrista Bent Larsen, em 1988).
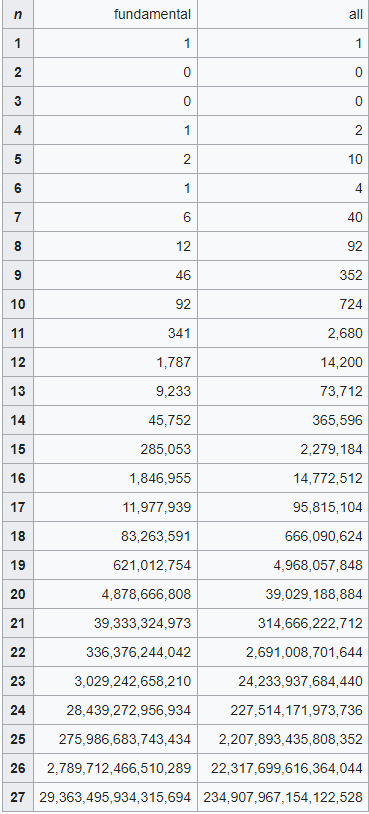
Figura 3 – Tabela exata de configurações. Na coluna ´fundamental´, temos todas as configurações, a menos de possíveis rotações e reflexões. Na coluna ´all ´, temos todas elas (Crédito: Ref. [7])
Mas, o grande embate homem x máquina aconteceu, quando o (então) campeão mundial de xadrez Garry Kasparov enfrentou (em seis partidas) o supercomputador Deep Blue (especialmente construído pela IBM). No primeiro confronto, em 1996, Kasparov venceu por 4 a 2 e, em 1997, perdeu por 3,5 a 2,5. Muito embora esses jogos tenham sido realizados com as regras normais de campeonatos (com relógio de tempo e tudo mais), Kasparov alegou estar em desvantagem, pois ele não teve acesso aos jogos recentes do Deep Blue, enquanto que este pôde consultar todos os seus jogos anteriores [5].
Em 2006, na Alemanha, o russo Vladimir Kramnik (que sucedeu Kasparov como campeão mundial de xadrez) recebeu 500.000 euros para enfrentar o programa de computador Deep Fritz. Ele receberia outros 500.00 euros, caso vencesse. O resultado de 4 a 2 para a máquina, selou (praticamente encerrou) a competição homem x computador. Nós não evoluímos tão rapidamente quanto os hardwares e softwares dos computadores… game is over [5].
É hora de voltarmos ao problema das damas. O mesmo Nauck que resolveu o problema das 8-damas em 1850, propôs a extensão desse problema para o caso de n damas num tabuleiro n x n [6]. As perguntas que precisavam ser respondidas eram as seguintes:
1) O problema das n-damas tem solução para qualquer n?
2) Quantas soluções existem?
Muitos e grandes matemáticos se debruçaram sobre o problema, incluindo C. F. Gauss.
A resposta para a primeira pergunta é mais fácil. Para todo n maior ou igual a 4 sempre haverá uma solução do tipo degrau de escada (veja Figura 2).
A resposta para a segunda pergunta só é conhecida (até hoje) para n menor ou igual a 27. Em 2016, um tour de force de computação paralela [7] conseguiu enumerar, exatamente, todas as possíveis configurações até n = 27 (veja Figura 3). O recorde anterior, com n = 26, havia sido obtido em 2010. Para n = 27, o número de configurações possíveis ultrapassa a marca incrível dos duzentos quatrilhões!
Um resultado fantástico. Mas, e se n for igual a mil ou um milhão? A resposta foi dada por um pós-doutorando no Center of Mathematical Sciences and Applications da Universidade de Harvard, Michael Simkin [8]. Ele trabalhou por mais de 5 anos no problema das n-damas e obteve uma fórmula assintótica para o número de configurações
(0,143 n) n
Se n for igual a um milhão, o resultado será um número com mais de cinco milhões de zeros!
*Físico, Professor Sênior do IFSC – USP
e-mail: onody@ifsc.usp.br
Para acessar todo o conteúdo do site “Notícias de Ciência e Tecnologia” dirija a câmera do celular para o QR Code abaixo

Compartilhe

(Agradecimento: ao Sr. Rui Sintra da Assessoria de Comunicação)
Referências:
[1] W. W. Rouse Ball (1960) “The Eight Queens Problem”, in Mathematical Recreations and Essays, Macmillan, New York, pp. 165–171.
[2] The eight queens puzzle in Python | Solarian Programmer
[3] The 10 Best Chess Players Of All Time – Chess.com
[4] International Chess Federation (fide.com)
[5] Human–computer chess matches – Wikipedia
[6] Eight queens puzzle – Wikipedia
[7]GitHub – preusser/q27: 27-Queens Puzzle: Massively Parellel Enumeration and Solution Counting
[8] [2107.13460] The number of $n$-queens configurations (arxiv.org)
Assessoria de Comunicação – IFSC/USP



