
Figura 1 – Visão artística do sistema estelar triplo Gliese 667 (ref. 1). Ele se encontra bem perto da Terra, a cerca de 22 anos-luz de distância, na direção da constelação de Escorpião. Hoje, no sistema Gliese 667, são conhecidos 6 exoplanetas, sendo que 3 deles se encontram em região habitável.exoplanetas, sendo que 3 deles se encontram em região habitável
Este artigo é a segunda parte do meu ensaio sobre o problema dos 3 corpos. A primeira parte você encontra aqui.
No seriado da Netflix “O problema dos três corpos” (baseado no livro de Liu Cixin) os 3 corpos fazem parte do sistema triplo de estrelas Alpha Centauri A, B e C.
As estrelas Alpha Centauri A e B têm, aproximadamente, o mesmo porte e luminosidade que o nosso Sol. Ambas estão a uma distância de 4,34 anos-luz do Sol e percorrem órbitas elípticas (em torno do centro de massa) com período de 79,7 anos.
A estrela Alpha Centauri C, mais conhecida como Proxima Centauri, se encontra a uma distância de 4,24 anos-luz e é a estrela mais próxima do Sol. É uma anã vermelha com apenas 12% da massa do Sol e 1% da sua luminosidade. Muito longe do centro de massa, seu período é enorme, cerca de 550 mil anos!
Proxima Centauri tem 2 exoplanetas conhecidos. Um deles, Proxima Centauri b, está na zona habitável e tem massa praticamente igual à da Terra. Com massa cem mil vezes menor do que Proxima Centauri e um milhão de vezes menor do que Alpha Centauri A e B, esse exoplaneta está entregue aos caprichos gravitacionais das 3 estrelas. No livro de Liu Cixin os alienígenas habitam um planeta denominado Trissolaris.
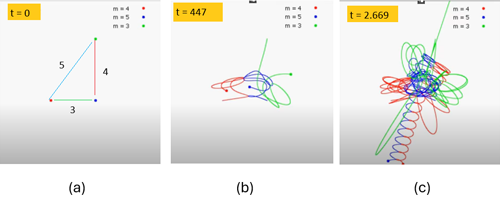
Figura 2 – Evolução temporal do problema Pitagórico dos 3 corpos. O autor utilizou a regularização de variáveis e o método de Runge-Kutta de 4ª. ordem para a integração numérica. Veja o vídeo (ref. 2)
Com 3 estrelas e 1 planeta habitado, o sistema é, de fato, um problema de 4 corpos restrito. Mas, claro, este não seria um bom título nem para o livro e nem para o seriado.
A desintegração do sistema de 3 corpos
Dependendo das posições e velocidades iniciais dos 3 corpos, é possível que o sistema venha a se desintegrar, isto é, um dos corpos venha a ser ejetado, expulso, afastando-se indefinidamente dos outros dois.
Um dos exemplos mais famosos é o chamado problema dos 3 corpos de Burraw, também conhecido como problema Pitagórico dos 3 corpos. Ele consiste em 3 corpos com massas 3, 4 e 5 (unidades arbitrárias) que se atraem gravitacionalmente. Todos estão inicialmente em repouso e posicionados nos vértices de um triângulo retângulo de lados 3, 4 e 5 (unidades arbitrárias). Problemas como esse, em que os 3 corpos têm velocidades iniciais nulas, são chamados de “queda livre” (free-fall).
No final do século 19, acreditava-se que esse sistema Pitagórico poderia apresentar soluções periódicas. Em 1913, Carl Burraw investigou o sistema e, sem os computadores de hoje, concluiu que não existia solução periódica para o problema.
De um ponto de vista matemático, o problema geral dos 3 corpos consiste em resolver um sistema de 18 equações diferenciais, acopladas e de 1ª. ordem no tempo. Como, no caso geral, não existe solução analítica, temos que recorrer ao computador para uma integração numérica.
Antes, porém, é necessário reescrever as equações em termos de variáveis mais apropriadas, num processo chamado de regularização. A regularização evita a explosão da interação gravitacional quando dois ou três desses corpos colidem.
Sabemos regularizar variáveis para colisões duplas, mas, não para colisões triplas. O teorema de Wintner demonstra que para haver uma colisão tripla é necessário, mas, não suficiente, que o momento angular do sistema seja nulo. Em outras palavras, as colisões triplas só podem acontecer em sistemas com momento angular nulo. E, mesmo nesses casos, elas podem não ocorrer já que as colisões triplas são extremamente improváveis. Para sistemas de 3 corpos em queda livre, foram estudados numericamente alguns casos em que há colisões triplas.
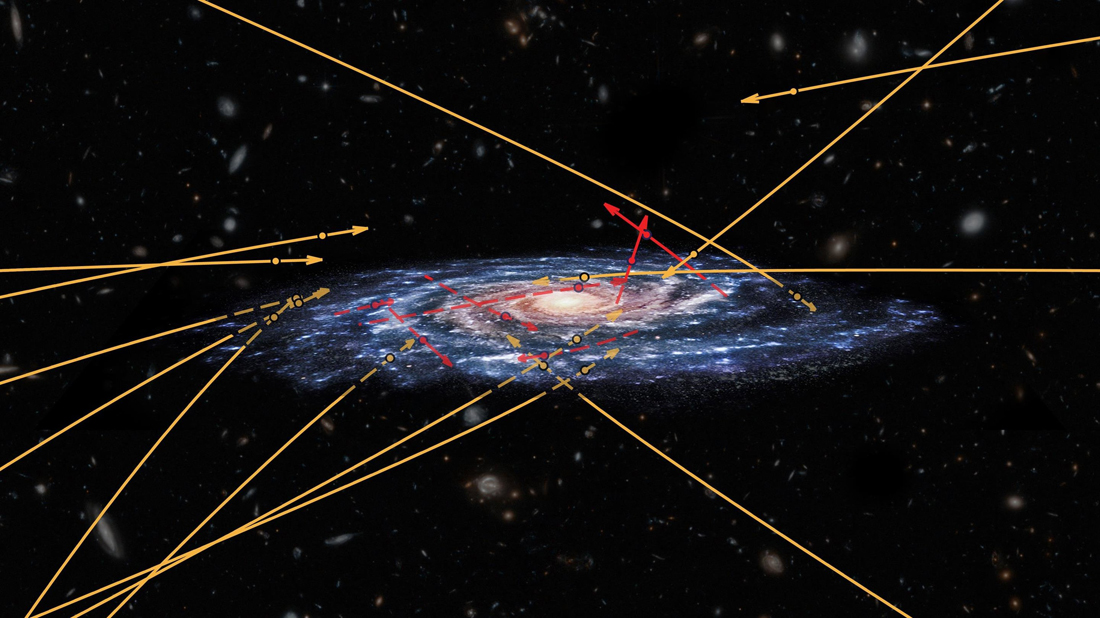
Figura 3 – O observatório espacial Gaia, lançado pela ESA (European Space Agency) em 2013, mapeou 20 estrelas com velocidades suficientes para sair ou entrar na Via Láctea. As setas vermelhas correspondem a estrelas sendo ejetadas da Via Láctea, as setas laranjas a estrelas provavelmente ejetadas por outras galáxias e penetrando a Via Láctea. A imagem é uma superposição artística da Via Láctea (ESA) com as posições e trajetórias reais das estrelas propostos no trabalho de Marchetti et al. (ref. 3)
Na Figura 2, vemos a evolução temporal do problema Pitagórico dos 3 corpos. (a) em t = 0, os corpos de massas 3, 4 e 5 estão em repouso nos vértices de um triângulo retângulo de lados 3, 4 e 5; (b) em t = 447, os 3 corpos executam uma coreografia complicada; (c) em t = 2.669, o corpo de menor massa (m=3) já foi ejetado, afastando-se (em linha reta) do sistema binário (m=4 e m=5) que, juntos, também se afastam, inexoravelmente, do centro de massa do sistema. O sistema de 3 corpos se desintegrou.
Em um trabalho muito interessante, Anosova e Orlov simularam em 3 dimensões um total de 9.500 sistemas de 3 corpos, com massas iguais e diferentes. Em seguida, eles fizeram um levantamento estatístico da probabilidade de desintegração dos 3 corpos como função do tempo e concluíram:
*A desintegração é um processo dominante e acontece em 85% dos casos!
*Em geral, a desintegração acontece logo após uma grande aproximação tripla dos corpos.
*A vida média desses processos disruptivos tem decaimento exponencial, lembrando muito os processos de decaimento radioativo.
*Quanto maior for o momento angular do sistema, maior será a sua vida média até a ruptura.
Usualmente, o corpo ejetado e o sistema binário têm orbitas não coplanares.
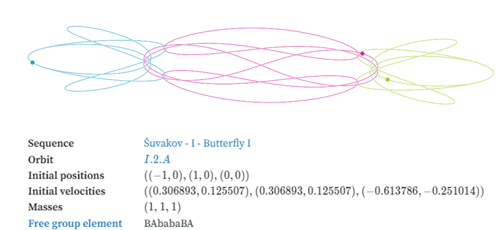
Figura 4 – A órbita periódica Butterfly I descoberta por Suvakov e Dimitrasinovic (ref. 4) em 2013. Em cima: os 3 corpos pontuais verde, vermelho e azul executam órbitas periódicas e suas respectivas trajetórias estão indicadas pelos rastos coloridos; Em baixo: as posições e velocidades iniciais no plano (x, y). O elemento do grupo livre é BAbabaBA (detalhes no material suplementar). Crédito: Ricky Reusser (ref. 5)
Geralmente, o corpo com menor massa é ejetado em alta velocidade. Buracos negros e estrelas podem formar sistemas que se desintegram com o tempo. As estrelas ejetadas podem adquirir hipervelocidades. Estima-se que, para um corpo celeste que habite a nossa região no espaço (estamos a cerca de 26 mil anos-luz do centro da Via Láctea), a velocidade de escape da Via Láctea é de aproximadamente 544 km/s.
Em 2005, foi descoberta a primeira estrela sendo ejetada a partir do halo da Via Láctea com velocidade aproximada de 853 km/s em relação ao Sol (Figura 3). A título de comparação, o Sol orbita o buraco negro supermassivo da Via Láctea com velocidade aproximada de 230 km/s.
Em busca das órbitas periódicas
Em 1890, H.Poincaré provou que o problema dos 3 corpos não é exatamente solúvel, isto é, dadas as posições e as velocidades iniciais dos corpos não é possível obtê-las num tempo posterior qualquer e expressá-las em termos de funções algébricas ou transcendentais. Além disso, ele identificou a enorme sensibilidade do sistema perante pequenas perturbações nas trajetórias dos corpos. Junto com o trabalho posterior de A.Liapunov , estavam lançadas as bases para o desenvolvimento da teoria do caos.
O conceito do caos foi popularizado na década de 1960 por K.Lorenz através do famoso ´efeito borboleta´ em que um furacão poderia se formar na América do Norte pelo simples bater das asas de uma borboleta na América do Sul. Foi também Lorenz que chamou a atenção para a importância de desenvolver algoritmos numéricos melhores posto que, em sistemas caóticos, os erros de truncagem se propagam de maneira exponencial!
No problema dos 3 corpos, no meio de uma infinidade de órbitas caóticas, encontram-se também as órbitas periódicas (tão importantes e tão desejadas pelos habitantes de Trissolaris).
Rotulando os 3 corpos por 1, 2 e 3, a descrição completa do movimento num determinado instante de tempo t é dada pelo conjunto de 6 vetores A(t)=[r1(t),r2(t),r3(t),v1(t),v2(t),v3(t)] onde os 3 primeiros são os vetores posição e os 3 últimos os vetores velocidade. O movimento é dito periódico e com período T se os 6 vetores se repetem em t+T.

Figura 5 – Em cima: órbita periódica descoberta pelo grupo de Shangai em 2018. A massa em vermelho vale metade das massas verde e azul; Em baixo: as posições e velocidades iniciais dos 3 corpos. O elemento do grupo livre é BaBAbA (veja material suplementar). Crédito: Ricky Reusser (ref. 5)
Trataremos aqui somente de órbitas periódicas planares, em que os 3 corpos permanecem sempre num mesmo plano. Para que isso aconteça, basta que todos os vetores de velocidades iniciais estejam no mesmo plano que contém os 3 corpos. Dessa maneira, o plano de movimentação dos 3 corpos é exatamente aquele perpendicular ao vetor momento angular total (que é constante no tempo).
O estudo do caso não planar com órbitas periódicas tridimensionais é muito mais difícil. Até onde eu sei, só se conhece a solução do problema circular restrito dos 3 corpos e a órbita cônica-helicoidal descoberta por Eugene Oks (veja mais adiante). Discutiremos as órbitas periódicas em ordem cronológica de suas descobertas.
As primeiras órbitas periódicas foram encontradas por Euler (em 1767) e por Lagrange (em 1772). Elas são as únicas soluções analíticas (exatas) conhecidas e os resultados valem para quaisquer valores das massas dos 3 corpos.
Na solução de Euler, os 3 corpos evoluem de maneira colinear (veja clipe 1); na solução de Lagrange, os 3 corpos evoluem sempre formando um triângulo equilátero (veja clipe 2).
O que acontece se aplicarmos pequenas perturbações nas órbitas de Euler e de Lagrange? As órbitas de Euler são instáveis e se degeneram. A órbita de Lagrange tem regiões estáveis (quando uma das massas é muito maior do que a dos outros 2 corpos), mas, é predominantemente instável. Instabilidade é exatamente o que acontece depois de longos ensaios em simulações numéricas devido aos inevitáveis erros de arredondamento. Os corpos abandonam suas órbitas periódicas e entram no regime caótico. Para ver isso, assista ao clipe 3 (Euler) e ao vídeo 1 (Lagrange).
Graças à conservação do vetor momento linear total, podemos sempre escolher um referencial inercial que está em repouso e tem origem no centro de massa.
Após as soluções encontradas por Euler e Lagrange foram necessários mais 200 anos até que surgissem novas soluções periódicas. Em meados da década de 1970, Broucke, Hénon e Hadjidemetriou (BHH) estudaram o caso em que os 3 corpos têm a mesma massa e se movimentam num plano (x, y).
As soluções periódicas de BHH no plano (x, y) têm as posições iniciais [(x1,0),(x2,0),(x3,0)] e velocidades iniciais [(0,v1),(0,v2),(0,v3)] , com x1+x2+x3=0 e v1+v2+v3=0.
Separei algumas das mais interessantes soluções periódicas de Broucke No clipe 4, todos os 3 corpos giram no sentido anti-horário e suas órbitas têm a forma de elos de uma corrente; no clipe 5, um dos corpos executa uma órbita circular no sentido anti-horário enquanto os outros 2 corpos percorrem, no sentido horário, um elegante trevo de 4 folhas; no clipe 6 temos uma solução periódica em que dois dos corpos seguem, de maneira subsequente, a mesma trajetória.
As soluções de Hénon são do tipo periódicas relativas, isto é, periódicas após uma rotação do plano (x, y) em torno do centro de massa. As órbitas periódicas de Broucke e Hénon são linearmente estáveis, o que significa que, perante pequenas perturbações (lineares) elas retornam à trajetória original.
Nossa próxima trajetória é a famosa e inacreditável órbita periódica que tem a forma de um oito (clipe 7). Hoje, ela é conhecida simplesmente como Figura 8. Nas simulações computacionais da Figura 8, os corpos têm posições iniciais [(-1,0),(0,0),(1,0)] e velocidade iniciais [(u, v),(-2u,-2v),(u, v)]. O momento angular total é zero. Como no caso das órbitas de BHH, a Figura 8 também é linearmente estável.
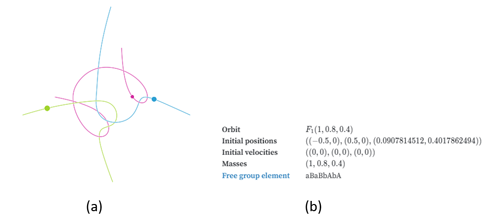
Figura 6 – (a) órbita periódica (descoberta em 2019) para 3 corpos com massas diferentes: 1, 0,8 e 0,4 (verde, azul e vermelho, respectivamente). Observe que em todos os casos os corpos vão e voltam na mesma trajetória; (b) as condições iniciais – os 3 corpos em queda livre. O elemento do grupo livre é aBaBbAbA (veja material suplementar). Crédito: Ricky Reusser (ref. 5)
Três corpos que se movimentam num plano bidimensional e evoluem no tempo, formam uma trança no espaço-tempo (2+1). Em 1993, Moore analisou este sistema de um ponto de vista topológico e encontrou a Figura 8. Em 2000, ela foi redescoberta numericamente por Chenciner e Montgomery.
No início do século 21 a busca por soluções periódicas do problema dos 3 corpos passava por dificuldades. Várias trajetórias consideradas ´novas´ eram, na verdade, redescobertas de órbitas já existentes (como no caso da Figura 8) ou meras transformações via translações e rotações. Era necessário encontrar uma maneira de classificá-las em classes ou famílias. Isso foi feito utilizando topologia e teoria de grupos.
Para não enveredar por um caminho muito complexo e matemático, preparei um material suplementar onde apresento detalhes do procedimento teórico. O leitor pode solicitar o material suplementar a onody@ifsc.usp.br. O suplemento está em pdf e será enviado por e-mail.
Em 2013, Suvakov e Dimitrasinovic da Universidade de Belgrado descobriram 13 novas famílias de soluções periódicas (veja Figura 4). Em 2014, eles publicaram um trabalho intitulado “A guide to hunting periodic three-body orbits”, onde eles discutem métodos para resolver as equações de movimento do problema dos 3 corpos planar e também as técnicas e estratégias para buscar órbitas periódicas. Esse grupo de Belgrado mantém uma página com os desenvolvimentos recentes da área.
Em 2017, entra em cena o grupo de Shangai. Eles catalogaram 695 novas famílias de soluções periódicas para sistemas de 3 corpos com massas iguais e momento angular zero. Em 2018, eles encontraram mais 1.349 famílias de órbitas periódicas para um sistema triplo composto por duas massas iguais e uma diferente (Figura 5).
Em seguida, em 2019, eles obtiveram 313 órbitas periódicas para um sistema de 3 corpos em queda livre (em que todos eles têm velocidades iniciais iguais a zero, veja Figura 6). Em 2023, um grupo internacional encontrou mais 24.582 novas órbitas periódicas para esses sistemas triplos com queda livre.
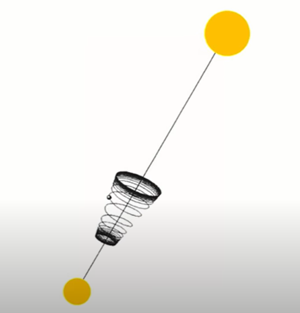
Figura 7 – O planeta tem uma órbita cônica-helicoidal que vai e vem ao longo do eixo que une as estrelas que compõem o sistema binário. As estrelas rotacionam em órbitas elípticas
E, finalmente, em 2021, o grupo de Shangai determinou outras 135.445 órbitas periódicas para sistemas com 3 massas diferentes. Com um número tão grande de órbitas, eles desenvolveram uma técnica de aprendizado de máquina para um modelo de rede neural que faz a busca por soluções periódicas.
Na minha opinião, apesar do grande esforço teórico e computacional realizado na última década, é muito improvável que as centenas de milhares de órbitas periódicas que já foram obtidas encontrem alguma realização no mundo real.
Há que se alterar duas hipóteses que foram assumidas para essas órbitas. Em primeiro lugar, os corpos celestes não são pontuais (e, em geral, nem esféricos) de forma que as forças gravitacionais devem ser calculadas por integração levando em conta a distribuição de densidade de cada corpo. Em segundo lugar, e mais importante, a imposição de uma órbita plana para os 3 corpos é uma demanda exagerada e inverossímil. Sim, porque por 3 pontos passa um único plano, mas, a condição de que os três vetores velocidade estejam, simultaneamente, num mesmo plano deve ser muitíssimo raro na natureza.
Aproveitando o que acabei de escrever acima, deixe-me apresentar uma órbita periódica tridimensional e estável que foi descoberta em 2015. Trata-se de um sistema de 3 corpos em que um planeta interage gravitacionalmente com um binário de estrelas (Figura 7). Ao longo do eixo interstelar, o planeta executa uma órbita cônica-helicoidal que oscila entre as duas estrelas. Veja no artigo de E. Oks o intervalo dos parâmetros gravitacionais no qual o sistema é periódico e estável.
Considerações finais
Indubitavelmente, o problema dos 3 corpos atraiu e continuará atraindo por muito tempo, um grande esforço teórico e computacional de muitos físicos e matemáticos talentosos. Confesso que fiquei surpreso com a beleza e a riqueza do problema dos 3 corpos. Abordar este tema foi um trabalho muito gratificante.
Por último, não posso deixar de mencionar o trabalho bacana do estudante de astrofísica da Universidade de La Laguna (Espanha), Pere Rosseló. Ele preparou um gif (clique aqui) com 20 órbitas periódicas que, pela sua estética e mesmerismo, serve como um cartão de visitas para o problema dos 3 corpos.
Clique abaixo para acessar as referências citadas nas figuras
*Físico, Professor Sênior do IFSC – USP
e-mail: onody@ifsc.usp.br
(Agradecimento: ao Sr. Rui Sintra da Assessoria de Comunicação)
Para acessar todo o conteúdo do site “Notícias de Ciência e Tecnologia”, clique aqui
Para acessar todo o conteúdo do site “Newsletter – Ciência em Panorama”, clique aqui
Assessoria de Comunicação – IFSC/USP



