
Figura-3: Srinivasa Ramanujan, um brilhante, talentoso e intuitivo matemático indiano que deixou dezenas de conjecturas matemáticas (Crédito: Wikipedia.org)
Por: Prof. Roberto N. Onody *
A razão áurea φ é conhecida desde Pitágoras e Euclides. As suas propriedades e características são amplamente apreciadas por artistas matemáticos, biólogos, arquitetos, músicos e até místicos (Figura 1). A razão áurea pode ser representada por uma fração contínua infinita e periódica (veja Figura 2). Como a razão áurea φ só tem números 1 em toda a sua fração contínua, ela é a mais difícil de ser aproximada por um número racional. Diz-se que φ é o mais irracional de todos os números irracionais.
É muito difícil apontar a origem das frações contínuas. A expressão fração contínua foi cunhada pelo matemático J. Wallis (1616-1703) e os primeiros resultados analíticos estão em seu livro Opera Mathematica (1695). Em 1761, J. H. Lambert utilizou a representação da função tg(x), em frações contínuas, para provar a irracionalidade do número π. Entretanto, foi L. Euler (1707-1783) quem demonstrou os principais fundamentos das frações contínuas:
-Todo número racionalpode ser escrito como uma fração contínua finita
-Todo número irracionalpode ser escrito como uma fração contínua infinita. Se ela for infinita, mas periódica, o número é uma raiz de uma equação quadrática com coeficientes racionais.
As frações contínuas são muito úteis para representar ou aproximar as constantes matemáticas1. As constantes matemáticas mais comuns como Pi (π=3,14…), Napier (e=2,71…) e Catalan (G=0,91…) são conhecidas com precisão quase arbitrária (número de dígitos). Já os valores das constantes físicas, como a carga do elétron, massa do próton, a constante da gravitação etc. são todas limitadas pelos próprios experimentos e pela resolução dos equipamentos.
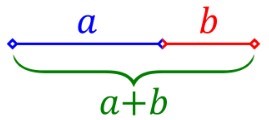
Figura-1: Num segmento de reta, considerando a>b>0, temos a proporção áurea definida por a/b = (a+b)/a. A razão áurea, φ = a/b, satisfaz a equação φ =1+1/φ, ou seja, φ = 1,618 (Crédito: R. N. Onody)
Outra característica importante das constantes matemáticas é que, na sua maioria, elas são números irracionais e, consequentemente, podem ser expressas como frações contínuas infinitas. Dois matemáticos geniais, C. F. Gauss (1777-1855) e S. A. Ramanujan (1887-1920), são muito conhecidos por encontrarem novas fórmulas e resultados de maneira profundamente intuitiva.
Gauss não tinha pressa de publicar seus resultados. Em 1796, com 19 anos, começou a escrever o seu diário científico, que só veio a público em 1898. Nele constavam mais de 140 fórmulas, muitas sem suas respectivas demonstrações. Gauss dizia que novas ideias trovejavam em sua cabeça e que as anotava por pura compulsão de sua natureza.
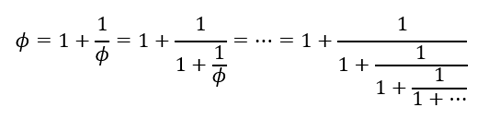
Figura-2: Substituindo φ iterativamente, chegamos à sua representação em função contínua infinita e periódica (Crédito: R. N. Onody)
Ramanujan (Figura 3), um incrível matemático indiano, também mantinha um caderno de anotações2. O caderno ficou perdido até 1976. Ao ser descoberto, revelou um total de 3.900 fórmulas e identidades matemáticas. Muitas dessas conjecturas, só foram comprovadas bem depois, utilizando conceitos e ideias inexistentes à época de Ramanujan. Sem formação acadêmica, enviou alguns resultados para o Prof. G. H. Hardy, da Universidade de Cambridge, que, reconhecendo o enorme talento de Ramanujan, conseguiu trazê-lo para a Inglaterra. Intuitivo, reconhecendo padrões matemáticos em todo lugar, tornou lendário um taxi britânico de número 1729. Ao entrarem no veículo, Hardy comentou que o número do taxi nada tinha de interessante, ao que Ramanujan retrucou “Tem sim. Ele é o menor número natural que é a soma de 2 cubos e de 2 maneiras diferentes”, pois 1729 = 13+123 = 93+103.
Um grupo de cientistas da Technion3 (Israel Institute of Technology, Haifa) publicou recentemente, na revista Nature, um algoritmo que sistematiza e propõe conjecturas de fórmulas matemáticas. Vale dizer, eles desejam dar um caráter computacional à criatividade e à intuição de Ramanujan. Para isso, eles construíram uma inteligência artificial à qual deram o nome de Máquina de Ramanujan.
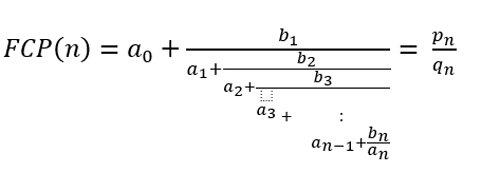
Figura-4: Frações Contínuas Polinomiais FCP(n), onde an= a(n) e bn= b(n) são polinômios em n, com coeficientes inteiros (Crédito: R. N. Onody)
A máquina de Ramanujam utiliza um algoritmo que foi, por eles batizado, de MITM (Meet-In-The-Middle) e realiza computação tanto numérica quanto algébrica. Suponha que desejamos expressar uma constante matemática c (por exemplo, c = π) em frações contínuas. Lembremos que o valor de c é, em geral, conhecido com uma precisão quase infinita. O algoritmo MITM pode ser resumido em 3 etapas.
Passo 1: escrevemos uma função racional
R(c) = S(c)/T(c)
onde S(c) e T(c) são polinômios em c, com coeficientes inteiros (arbitrariamente grandes). Escolhe-se uma precisão inicial para c (digamos, 10 casas decimais). Constrói-se um número gigantesco de funções racionais {R(c)}, varrendo-se o valor de seus coeficientes inteiros e o grau do polinômio. Cada elemento do conjunto {R(c)} tem o seu valor numérico calculado e armazenado numa tabela de dispersão (hash table).
Passo 2: usando computação paralela, trabalha-se agora com as Frações Contínuas Polinomiais FCP(n) (Figura 4). Aqui, an = a(n) e bn = b(n) são funções polinomiais (de n) com coeficientes inteiros (arbitrariamente grandes). Se n é um número finito, as FCP(n) sempre podem ser escritas como uma função racional, cujo numerador parcial pn e denominador parcial qn são obtidos recursivamente
pn+1 = an+1 pn + bn+1 pn-1 ; com p-1 = 1 e p0 = a0
qn+1 = an+1 qn + bn+1 qn-1 ; com q-1 = 0 e q0 = 1
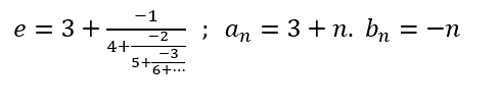
Figura-5: A constante de Napier em Frações Contínuas Polinomiais. Pode ser calculada com a precisão desejada, truncando-se, para um certo n = N, as recorrências dos numeradores e denominadores parciais pn e qn (Crédito: R. N. Onody)
Varrendo-se os coeficientes inteiros e o grau dos polinômios a(n) e b(n), constrói-se um conjunto {FCP(N)}, onde N é o número de iterações necessárias para que, cada elemento, seja calculado com precisão de 10 casas decimais.
Passo 3: Comparando-se os valores numéricos dos conjuntos {R(c)} e {FCP(N)}, aqueles que coincidirem (até 10 casas decimais) são escolhidos para recomeçar todo o processo. O valor da constante matemática c é substituído por um novo valor c’, com precisão maior (por exemplo, de 20 dígitos). Retorna-se ao Passo 1. Dessa maneira, soluções falso positivas em c serão eliminadas em c’.
Os autores prosseguiram o algoritmo MITM até a precisão de 2.000 dígitos! Eles obtiveram dezenas de novas expressões para uma variedade de constantes matemáticas e, muitas delas, com convergência mais rápida. Para deixar tudo um pouco mais claro, ilustramos na Figura 5, o caso da constante de Napier e (a expressão, conjecturada pela máquina de Ramanujan, já foi demonstrada teoricamente).
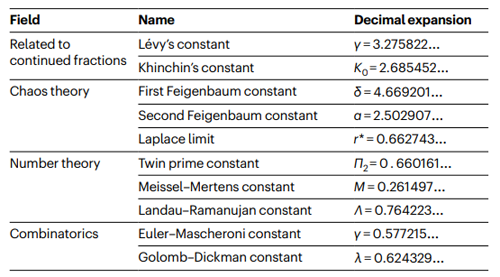
Figura-6: Algumas constantes matemáticas que os autores da pesquisa gostariam de ver analisadas pela máquina de Ramanujan
(Crédito: 3 G. Raayoni et al)
Outra constante matemática, sobre a qual eles se debruçaram, foi a constante de Catalan G. Até hoje, não se sabe se G é um número irracional ou não. Os pesquisadores encontraram várias representações de G em frações contínuas generalizadas. Por exemplo, uma expressão, ainda sem demonstração teórica, é a seguinte
2/(2G-1) = FCP [an = 3+n(7+3n), bn = – (6+2n)(n+1)3 ], n=0,1,2,..
Claro, todo o processo MITM requer muito esforço computacional. À semelhança do que acontece com a busca internacional dos números primos de Mersenne4, todo o projeto (códigos e resultados atualizados) foi disponibilizado ao público no site http://www.ramanujanmachine.com/.
Na Figura 6, apresentamos algumas constantes matemáticas que, os autores do artigo, gostariam de ver investigadas pela máquina de Ramanujan.
Mais do que em qualquer outra ciência, a matemática possui conjecturas famosas em grande profusão. Propostas por matemáticos geniais e intuitivos, as conjecturas têm um papel muito importante em toda a história e o desenvolvimento da matemática. Quer elas já tenham sido demonstradas ou não (ou, eventualmente descartadas, caso inverídicas), as conjecturas matemáticas têm enorme potencial de atrair, fascinar e motivar pessoas, aglutinando e gerando novos conhecimentos.
*Físico, Professor Sênior do IFSC – USP
(Agradecimento: ao Sr. Rui Sintra da Assessoria de Comunicação)
Referências:
1 S. Finch, Mathematical Constants (Cambridge Univ. Press, 2003).
2 B. C. Berndt, Ramanujan’s Notebooks (Springer Science & Business Media, 2012).
3 G. Raayoni et al. Nature, 590, 67-73 (2021)
https://www.nature.com/articles/s41586-021-03229-4
Assessoria de Comunicação – IFSC/USP



