Classical geometric fluctuation relations.
MELO, Pedro Barreto; QUEIRÓS, Sílvio Manuel Duarte; PINTO, Diogo de Oliveira Soares; MORGADO, Welles Antonio Martinez.
MELO, Pedro Barreto; QUEIRÓS, Sílvio Manuel Duarte; PINTO, Diogo de Oliveira Soares; MORGADO, Welles Antonio Martinez.
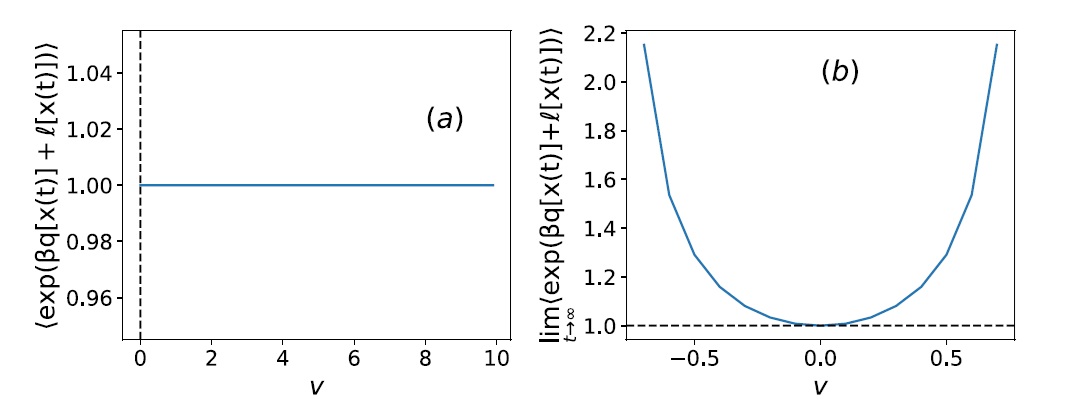Abstract: Fisher Information (FI) is a quantity ubiquitously measured in such varied areas like metrology, machine learning, and biological complexity. Mathematically, it represents a lower bound in the variance of unknown parameters that are related to the distributions one has access, and a metric for probability manifolds. A stochastic analogous of the FI, dubbed stochastic FI was recently introduced in the literature by some of us. By exploring the probability distributions of the stochastic FI (SFI), we uncover two fluctuation relations with an inherent geometric nature, as the SFI acts as a single nonequilibrium trajectory metric. The geometric nature of these relations is expressed through a stochastic length in entropy space derived from the system entropy associated with a nonequilibrium trajectory. We also explore the possibility of trajectory-dependent uncertainty relations linked to the SFI with time as a parameter. Finally, we test our geometric fluctuation relations using two nonequilibrium models.
@article={003251301,author = {MELO, Pedro Barreto; QUEIRÓS, Sílvio Manuel Duarte; PINTO, Diogo de Oliveira Soares; MORGADO, Welles Antonio Martinez.},title={Classical geometric fluctuation relations},journal={Journal of Physics A},note={v. 58, n. 19, p. 195001-1-195001-14},year={2025}}