Spacing ratio characterization of the spectra of directed random networks.
PERON, Thomas Kauê Dal'Maso; RESENDE, Bruno Messias Farias de; RODRIGUES, Francisco Aparecido; COSTA, Luciano da Fontoura; MÉNDEZ-BERMÚDEZ, J. A.
PERON, Thomas Kauê Dal'Maso; RESENDE, Bruno Messias Farias de; RODRIGUES, Francisco Aparecido; COSTA, Luciano da Fontoura; MÉNDEZ-BERMÚDEZ, J. A.
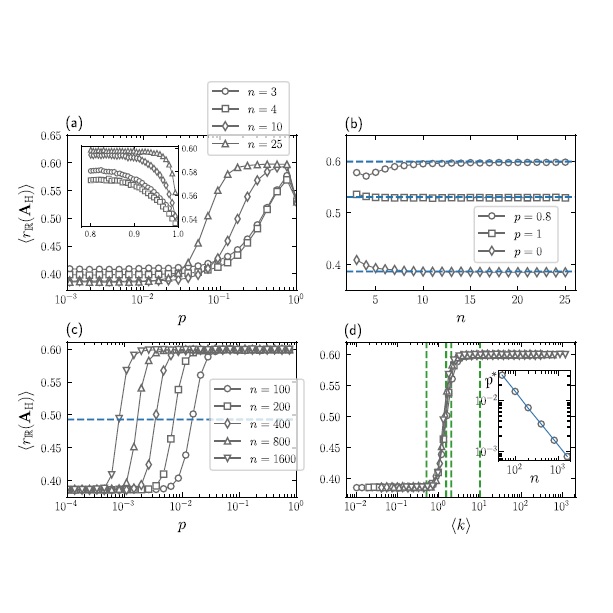Abstract: Previous literature on random matrix and network science has traditionally employed measures derived from nearest-neighbor level spacing distributions to characterize the eigenvalue statistics of random matrices. This approach, however, depends crucially on eigenvalue unfolding procedures, which in many situations represent a major hindrance due to constraints in the calculation, especially in the case of complex spectra. Here we study the spectra of directed networks using the recently introduced ratios between nearest and next-to-nearest eigenvalue spacing, thus circumventing the shortcomings imposed by spectral unfolding. Specifically, we characterize the eigenvalue statistics of directed Erd?os-Rényi (ER) random networks by means of two adjacency matrix representations, namely, (1) weighted non-Hermitian random matrices and (2) a transformation on non-Hermitian adjacency matrices which produces weighted Hermitian matrices. For both representations, we find that the distribution of spacing ratios becomes universal for a fixed average degree, in accordance with undirected random networks. Furthermore, by calculating the average spacing ratio as a function of the average degree, we show that the spectral statistics of directed ER random networks undergoes a transition from Poisson to Ginibre statistics for model 1 and from Poisson to Gaussian unitary ensemble statistics for model 2. Eigenvector delocalization effects of directed networks are also discussed.
@article={003014235,author = {PERON, Thomas Kauê Dal'Maso; RESENDE, Bruno Messias Farias de; RODRIGUES, Francisco Aparecido; COSTA, Luciano da Fontoura; MÉNDEZ-BERMÚDEZ, J. A.},title={Spacing ratio characterization of the spectra of directed random networks},journal={Physical Review E},note={v. 102, n. 6, p. 062305-1-062305-9},year={2020}}