Malleability of complex networks.
SILVA, Filipi Nascimento; COMIN, Cesar H.; COSTA, Luciano da Fontoura.
SILVA, Filipi Nascimento; COMIN, Cesar H.; COSTA, Luciano da Fontoura.
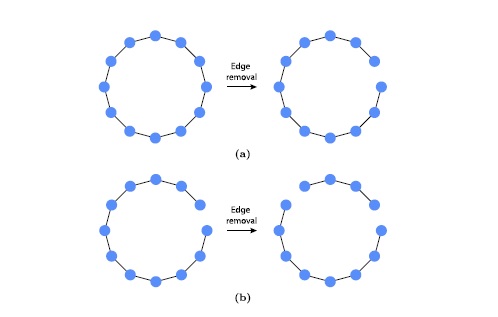 Abstract: Most complex networks are not static, but evolve along time. Given a specific configuration of one such changing network, it becomes a particularly interesting issue to quantify the diversity of possible unfoldings of its topology. In this work, we suggest the concept of malleability of a network, which is defined as the exponential of the entropy of the probabilities of each possible unfolding with respect to a given network configuration. In order to avoid the combinatorics involved by identifying isomorphisms, we calculate the malleability with respect to specific measurements of the involved topologies. More specifically, we identify the possible topologies derivable from a given configuration and calculate some topological measurements of them, such as clustering coecient, shortest path length and assortativity, leading to respective probabilities being associated to each possible measurement value. Though this approach implies some level of degeneracy in the mapping from topology to measurement space, it still paves the way to inferring the malleability of specific network types with respect to given topological measurements. We report that the malleability, in general, depends on each specific measurement, with the average shortest path length and degree assortativity typically being characterized by large malleability values. For an edge removal dynamics, large malleability values were observed for the Barabási?Albert, ErdosRényi and Waxman network models, while the Watts?Strogatz model resulted in the smallest malleability values. Abstract: Most complex networks are not static, but evolve along time. Given a specific configuration of one such changing network, it becomes a particularly interesting issue to quantify the diversity of possible unfoldings of its topology. In this work, we suggest the concept of malleability of a network, which is defined as the exponential of the entropy of the probabilities of each possible unfolding with respect to a given network configuration. In order to avoid the combinatorics involved by identifying isomorphisms, we calculate the malleability with respect to specific measurements of the involved topologies. More specifically, we identify the possible topologies derivable from a given configuration and calculate some topological measurements of them, such as clustering coecient, shortest path length and assortativity, leading to respective probabilities being associated to each possible measurement value. Though this approach implies some level of degeneracy in the mapping from topology to measurement space, it still paves the way to inferring the malleability of specific network types with respect to given topological measurements. We report that the malleability, in general, depends on each specific measurement, with the average shortest path length and degree assortativity typically being characterized by large malleability values. For an edge removal dynamics, large malleability values were observed for the Barabási?Albert, ErdosRényi and Waxman network models, while the Watts?Strogatz model resulted in the smallest malleability values. | |
| Journal of Statistical Mechanics |
| v. 2019, p. 083203-1-083203-15 - Ano: 2019 |
| Fator de Impacto: 2,371 |
| http://dx.doi.org/10.1088/1742-5468/ab2ad1 |  @article={002959776,author = {SILVA, Filipi Nascimento; COMIN, Cesar H.; COSTA, Luciano da Fontoura.},title={Malleability of complex networks},journal={Journal of Statistical Mechanics},note={v. 2019, p. 083203-1-083203-15},year={2019}} @article={002959776,author = {SILVA, Filipi Nascimento; COMIN, Cesar H.; COSTA, Luciano da Fontoura.},title={Malleability of complex networks},journal={Journal of Statistical Mechanics},note={v. 2019, p. 083203-1-083203-15},year={2019}} |



