Quasi-integrability of deformations of the KdV equation.
BRAAK, F. ter; FERREIRA, Luiz Agostinho; ZAKRZEWSKI, W. J.
BRAAK, F. ter; FERREIRA, Luiz Agostinho; ZAKRZEWSKI, W. J.
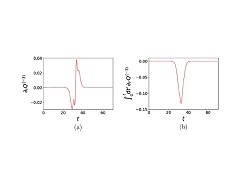 Abstract: We investigate the quasi-integrability properties of various deformations of the Korteweg-de Vries (KdV) equation, depending on two parameters e1 and e2, which include among them the regularized long-wave (RLW) and modified regularized long-wave (mRLW) equations. We show, using analytical and numerical methods, that the charges, constructed from a deformation of the zero curvature equation for the KdV equation, are asymptotically conserved for various values of the deformation parameters. By this we mean that, despite the fact that the charges do vary in time during the scattering of solitons, they return after the scattering to the same values they had before it. This property was tested numerically for the scattering of two and three solitons, and analytically for the scattering of two solitons in the mRLW theory (e2=e1=1). In addition we show that for any values of e1 and e2 the Hirota method leads to analytical one-soliton solutions of our deformed equation but for e1?1 such solutions have the dispersion relation which depends on the parameter e1. We also discuss some properties of soliton-radiation interactions seen in some of our simulations. Abstract: We investigate the quasi-integrability properties of various deformations of the Korteweg-de Vries (KdV) equation, depending on two parameters e1 and e2, which include among them the regularized long-wave (RLW) and modified regularized long-wave (mRLW) equations. We show, using analytical and numerical methods, that the charges, constructed from a deformation of the zero curvature equation for the KdV equation, are asymptotically conserved for various values of the deformation parameters. By this we mean that, despite the fact that the charges do vary in time during the scattering of solitons, they return after the scattering to the same values they had before it. This property was tested numerically for the scattering of two and three solitons, and analytically for the scattering of two solitons in the mRLW theory (e2=e1=1). In addition we show that for any values of e1 and e2 the Hirota method leads to analytical one-soliton solutions of our deformed equation but for e1?1 such solutions have the dispersion relation which depends on the parameter e1. We also discuss some properties of soliton-radiation interactions seen in some of our simulations. | |
| Nuclear Physics B |
| v. 939, p. 49-94 - Ano: 2019 |
| Fator de Impacto: 3,285 |
| http://dx.doi.org/10.1016/j.nuclphysb.2018.12.004 |  @article={002917899,author = {BRAAK, F. ter; FERREIRA, Luiz Agostinho; ZAKRZEWSKI, W. J.},title={Quasi-integrability of deformations of the KdV equation},journal={Nuclear Physics B},note={v. 939, p. 49-94},year={2019}} @article={002917899,author = {BRAAK, F. ter; FERREIRA, Luiz Agostinho; ZAKRZEWSKI, W. J.},title={Quasi-integrability of deformations of the KdV equation},journal={Nuclear Physics B},note={v. 939, p. 49-94},year={2019}} |



