Paradoxical extension of the edge states across the topological phase transition due to emergent approximate chiral symmetry in a quantum anomalous Hall system.
CANDIDO, Denis R.; KHARITONOV, Maxim; EGUES, José Carlos; HANKIEWICZ, Ewelina M.
CANDIDO, Denis R.; KHARITONOV, Maxim; EGUES, José Carlos; HANKIEWICZ, Ewelina M.
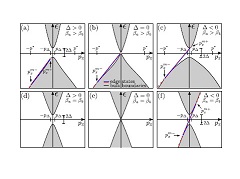 Abstract: We present a paradoxical finding that, in the vicinity of a topological phase transition in a quantum anomalous Hall system (Chern insulator), topology nearly always (except when the system obeys charge-conjugation symmetry) results in a significant extension of the edge-state structure beyond the minimal one required to satisfy the Chern numbers. The effect arises from the universal gapless linear-in-momentum Hamiltonian of the nodal semimetal describing the system right at the phase transition, whose form is enforced by the change of the Chern number. Its emergent approximate chiral symmetry results in an edge-state band in the vicinity of the node, in the region of momenta where such a form is dominant. Upon opening the gap, this edge-state band is modified in the gap region, becoming "protected" (connected to the valence bulk band with one end and conduction band with the other) in the topologically nontrivial phase and "nonprotected" (connected to either the valence or conduction band with both ends) in the trivial phase. The edge-state band persists in the latter as long as the gap is small enough. | |
| Physical Review B |
| v. 98, n. 16, p. 161111-1-161111-5 - Ano: 2018 |
| Fator de Impacto: 3,813 |
| http://dx.doi.org/10.1103/PhysRevB.98.161111 |  @article={002908630,author = {CANDIDO, Denis R.; KHARITONOV, Maxim; EGUES, José Carlos; HANKIEWICZ, Ewelina M.},title={Paradoxical extension of the edge states across the topological phase transition due to emergent approximate chiral symmetry in a quantum anomalous Hall system},journal={Physical Review B},note={v. 98, n. 16, p. 161111-1-161111-5},year={2018}} |