Multidimensional elephant random walk with coupled memory.
MARQUIONI, Vitor M.
MARQUIONI, Vitor M.
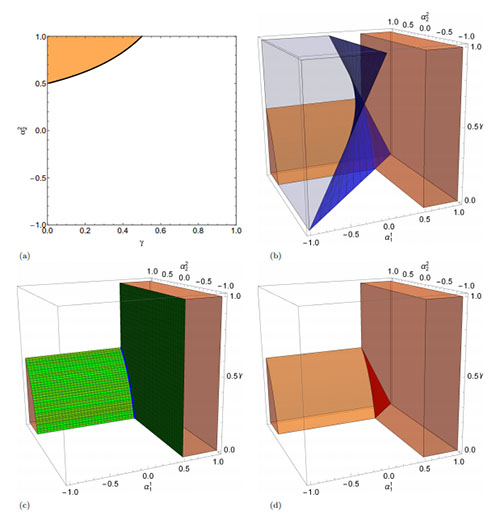 Abstract: The elephant random walk (ERW) is a microscopic, one-dimensional, discrete-time, non-Markovian random walk, which can lead to anomalous diffusion due to memory effects. In this study, I propose a multidimensional generalization in which the probability of taking a step in a certain direction depends on the previous steps in other directions. The original model is generalized in a straightforward manner by introducing coefficients that couple the probability of moving in one direction with the previous steps in all directions. I motivate the model by first introducing a two-elephant system and then elucidating it with a specific coupling. With the explicit calculation of the first moments, I show the existence of two newsworthy relative movement behaviors: one in which one elephant follows the other and another in which they go in opposite directions. With the aid of a Fokker-Planck equation, the second moment is evaluated and two superdiffusion regimes appear, not found in other ERWs. Then, I reinterpret the equations as a bidimensional elephant random walk model, and further generalize it to N dimensions. I argue that the introduction of coupling coefficients is a way of extending any one-dimensional ERW to many dimensions. | |
| Physical Review E |
| v. 100, n. 5, p. 052131-1-052131-10 - Ano: 2019 |
| Fator de Impacto: 2,353 |
| https://doi.org/10.1103/PhysRevE.100.052131 |  @article={002980683,author = {MARQUIONI, Vitor Marquioni.},title={Multidimensional elephant random walk with coupled memory},journal={Physical Review E},note={v. 100, n. 5, p. 052131-1-052131-10},year={2019}} |